Solder form
See wikipedia.
Definition
Let $M$ be a smooth manifold, and $G$ a Lie group. Let $E\to M$ be a fiber bundle with structure group $G$ (see G-bundles). Suppose that $G$ acts transitively on the standard fibre $F$, and that $dim F=dim M$. (By the way, the standard fibre would be a homogeneous space).
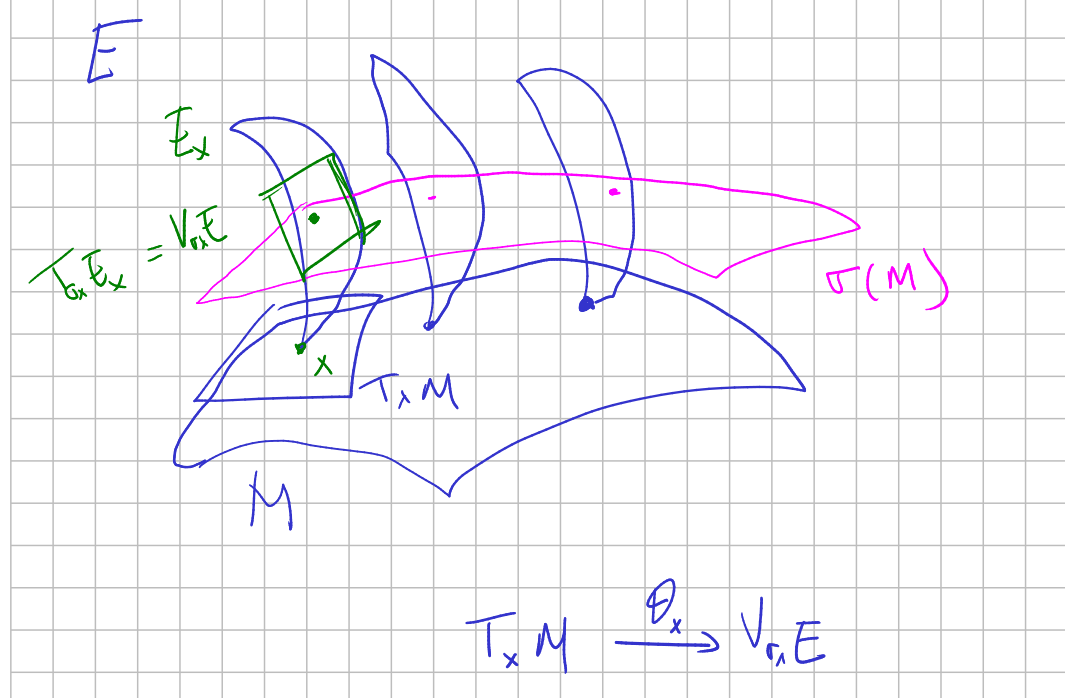
A soldering of $E$ to $M$ consist of:
- A distinguished section $\sigma: M\to E$.
- A linear isomorphism of vector bundles
from the tangent bundle of $M$ to the pullback of the vertical bundle of $E$. This is called the solder form.
$\blacksquare$
The intuition behind this notion is $E$ represents putting a copy of a homogeneous space on every point of $M$, and the soldering tell us a point of contact for every $x$ with the homogeneous space and an identification of the tangent spaces.
Principal bundles
See wikipedia, down to "principal bundles" section.
Suppose that $M$ has dimension $n$ and $H$ is a group which acts on $\mathbb{R}^n$ (i.e., we have a group representation of $H$). A solder form on a $H$-principal bundle $P$ over $M$ is an $\mathbb{R}^n$-valued 1-form $\theta: TP \to \mathbb{R}^n$ which is horizontal (in the sense that $\theta(V)=0$ for $V$ a vertical vector) and equivariant
$$ R_h^*\theta=h^{-1}\theta $$for $h\in H$; so that it induces a bundle homomorphism from TM to the associated bundle $P \times_{H} \mathbb{R}^{n}$. This is furthermore required to be a bundle isomorphism.
The reason for the name is that a solder form solders (or attaches) the abstract principal bundle to the manifold M by identifying an associated bundle with the tangent bundle.
The main example is the canonical solder form of the frame bundle, which sends a tangent vector $X\in T_pP$ to the coordinates of $d\pi_p(X)\in T_{\pi(p)}M$ with respect to the frame $p$.
________________________________________
________________________________________
________________________________________
Author of the notes: Antonio J. Pan-Collantes
INDEX: